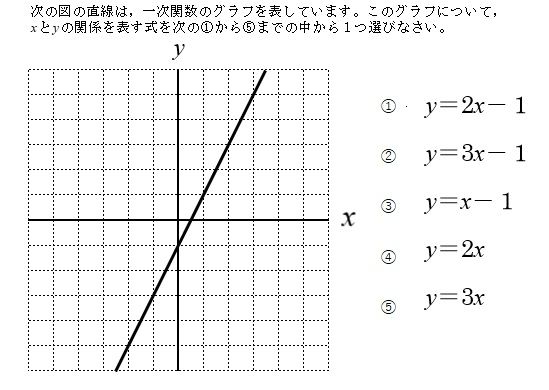
関数のグラフの中にある三角形で 3つの頂点の座標が分かる場合の 三角形の面積の求め方に なります。 高校入試でも よく出題されるところなので しっかりと マスターしておきましょう! まとめ 関数のグラフの中にある 三角形の面積を求めるコツ前回 https//wwwyoutubecom/watch?v=JyiWzS7Og&list=PLKRhhk0lEyzNXjYxLcVJBDQMnGQ9EJDEJ&index=39 次回 https//wwwyoutubecom/watch?v=hM_VhOlQeso&list初等関数 ジョゼフ・リウヴィルは初等関数を次のように定義した。 多項式を第 0 級初等関数、指数関数 e z と対数関数 log(z) を第 1 級初等関数、両者をあわせて、たかだか第 1 級初等関数と呼ぶ。 以下、関数の合成を行うことで、たかだか第 n 級初等関数を帰納的に構成できる。
中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
数学 関数 グラフ 一覧
数学 関数 グラフ 一覧-導関数のグラフを描く準備 グラフを描く前に、方程式自体を検討すればその性質を見出すことができます。 この数学概念は難しそうに見えるけど、きっと理解できるようになる!(出典:Ben White, ) カッコの一つは (x3) です。 関数のグラフの拡大の公式 y = f ( x ) y=f(x) y = f ( x ) のグラフを,原点中心に x x x 軸方向に A A A 倍, y y y 軸方向に B B B 倍すると, x x x を x A \dfrac{x}{A} A x に変えて y y y を y B \dfrac{y}{B} B y に変えた 以下の関数になる:



中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su
指数関数④ y=ex² のグラフ(正規分布曲線もどき) 指数関数⑤ y=e 1/x のグラフ; 指数関数のグラフの二通りの書き方 このページでは,指数関数のグラフの書き方を詳しく解説します。 y=12\cdot 3^ {x1} y = 12⋅ 3x−1 などのグラフをすばやく書けるようにしま関数グラフ GeoGebra グラフ作成専用Webアプリ(関数グラフ、方程式の探究、データのプロット、スライダー利用、等々) 関数グラフ
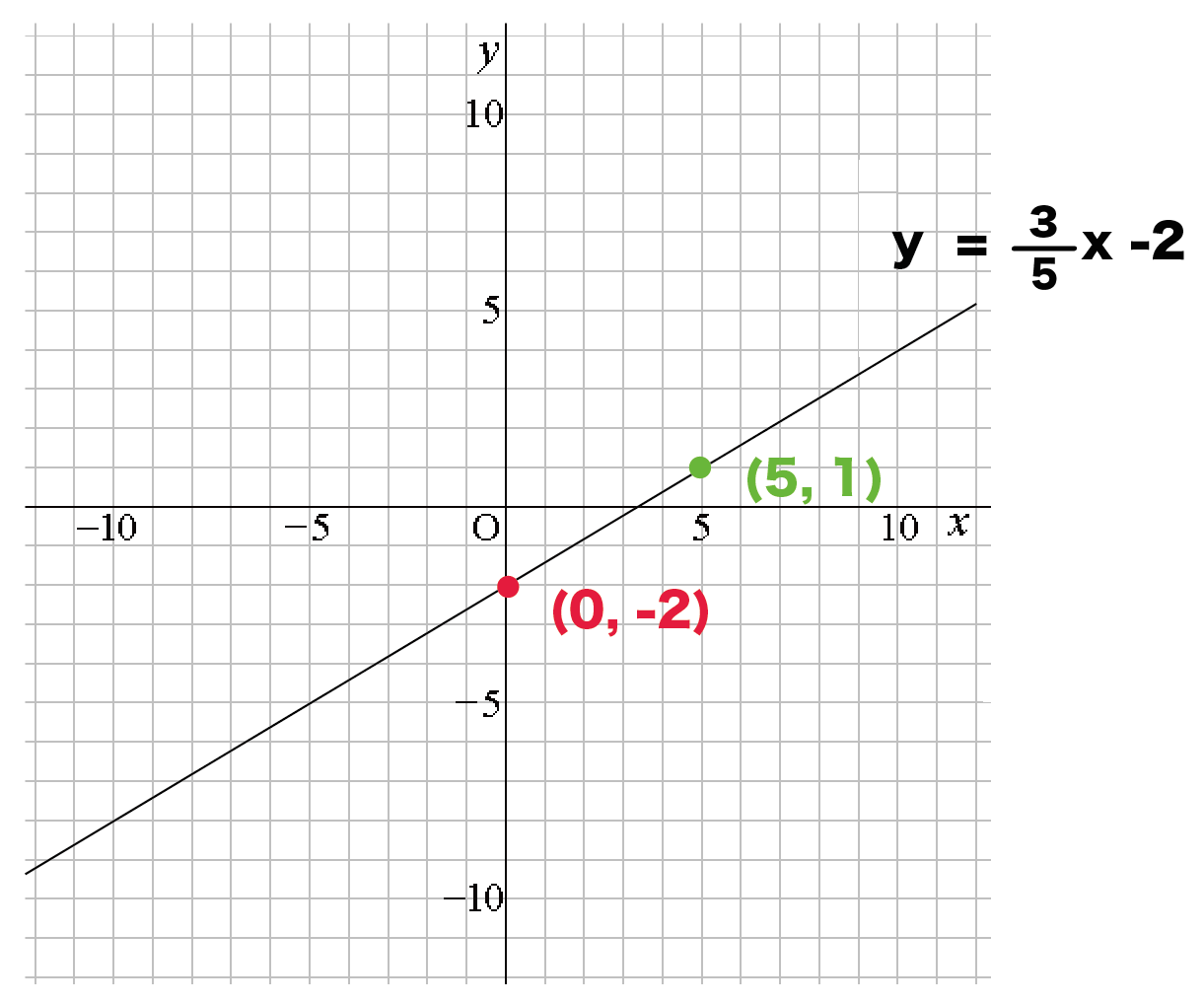
そしてグラフから一次関数の式を読み取ることもできます。 「x x に対するy y の増加量」 が 傾き 、 「y y 軸と交わる点のy y 座標の値」 が 切片 です。指数関数⑥ y=x x のグラフ(対数微分法) 双曲線関数 y=(e x ex)/2(カテナリー;懸垂線)と y=(e xex)/2 のグラフ (指数関数)×(三角関数) y=ex sinx のグラフ(減衰曲線) 対数関数① y=xlogx のグラフ;指数関数③ y=x/e x =xex のグラフ;
GeoGebra 関数グラフ 関数を簡単にグラフ化し、方程式を解き、関数の特別な点を見つけ、結果を保存して共有します。 世界中の何百万人もの人々が数学と科学を学ぶためにGeoGebraを使用しています。 参加しませんか! 私たちはあなたからのご意見をお待ち 定期テストで、試験範囲になっていれば、100%出題されるところです。しっかりおさえていきましょう。2次関数のグラフの特徴 原点を通る(頂点は、原点である) y軸に対称 放物線になる a>0のとき、上に開く。a<0のとき、下に開く。 一次関数のグラフはとても単純でした。 直線が、斜めに走っているだけです。 そのため、二次関数のグラフは、一次関数のグラフとはまるで別物のように感じる人も少なくありません。 しかしグラフも「 二次関数は一次関数から 1 つ増えただけ 」です。



1



Onenote の数学用アシスタントで関数のグラフを描画する
10ミリと5ミリの方眼ノートと、数学で関数のグラフをかく練習をするのに便利な数学の関数グラフ練習用方眼ノートです。 「数学の関数グラフ練習用方眼ノート」は、管理人が中学2年生の娘とテスト勉強を一緒にやっている時に、1次関数のグラフをかく練習をやりたくて作りました。 このページの用紙はすべてサイズです。 方眼の目盛りの10ミリ、5ミリのサイズ Recipe『各関数のグラフ』 高校生 数学のノート Clear 表紙 1 2 公開日時 14年11月04日 19時02分 更新日時 21年06月12日 01時49分 高校生 数学有理関数のグラフの書き方 タイプ: 教科書範囲 レベル: ★★ 有理関数 (分母分子が多項式の分数関数)の増減,そして 凹凸 まで調べたグラフの書き方について,説明します. 基本的に, 凹凸まで調べた増減表とグラフの書き方 の知識を使います



濃い罫線版 方眼紙 5ミリ 10ミリ 数学の関数グラフ練習用 方眼ノート 無料ダウンロード ちびむすドリル 小学生



中2数学 一次関数のグラフ を作成 おっくうの教材作成日記 楽天ブログ
四次関数のグラフの概形と例題2問 四次関数のグラフの特徴,書き方について解説します。四次関数は,教科書では数学2の発展事項として扱われています。 → 四次関数のグラフの概形と例グラフは, 最大値・最小値を求める問題や方程式の実数解に関する問題などいろいろな問題で利用します。また, 入試などでも「グラフをかけ。」という問題が出題されているので, 上のまとめにあるポイントを押さえて, どのようなグラフでもかけるように, 練習しておきましょう。 中学関数のグラフは3パターンのみ 中学校で習う関数のグラフは、ずばり、次の 3つの形 しかありません! ・直線 (比例、一次関数) ・双曲線 (反比例) ・放物線 ( y = ax2 ) ↑ 比例のグラフ( 直線 ) ?↑ 一次関数のグラフ( 直線 )



二次関数グラフの作成 数学 東三



Excelでグラフ
指数関数② y=x²e x のグラフ;「1次関数」 は式をグラフにすると 「直線」 に、 「2次関数」 は式をグラフにすると 「放物線」 になるよ。 こうしてグラフを見れば、xの値が変わっていったとき、それに合わせてyの値がどう増えるのか減るのか、パッと見ただけで分かるよね。代数ダンスおかしい関数グラフ図科学数学方程式 Tシャツ 5つ星のうち46 149個の評価 価格 ¥2,097 & 返品無料 この商品は返品無料です 試着後も商品到着後30日以内であれば商品代金(税込)および国内返送料を返金します。 詳しい条件はこちら 返品手順




三角関数です Y切片の求め方が分かりません Clear




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ
2次関数のグラフ(放物線)を動かしてみよう! 様々といっても,基本的には高等学校の数学で扱う関数 − − − 整関数,有理関数,無理関数,三角関数,指数関数,対数関数 こんなところです 例えば,頂点の軌跡はどうなっているのだろうか? 上変化の割合 = 傾き 1次関数 y= axb y = a x b において、 a a は、直線の傾きを表している ことを上で見ました。 この a a には別名があり、 変化の割合 といいます。 変化の割合とは、グラフがどのように変化しているのかを示す値で、 変化の割合 = yの動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
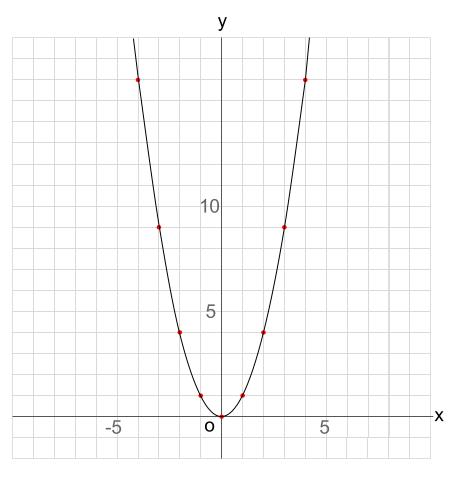



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su



グラフ用紙上の座標の三角法系 ベクターイラスト 三角関数のグラフを描画する空のテンプレート 青のチェッカー紙に黒い軸 数学的デザイン のベクター画像素材 ロイヤリティフリー
3.様々な関数とグラフ 3.1 高次関数(1次、2次、3次、4次関数まで) 1次関数、2次関数は中学数学、3次関数、4次関数は高校数学で扱うかと思います。 そこで本節では、1次~4次関数までを対象にして、学習用のシートを作成してみましょう。
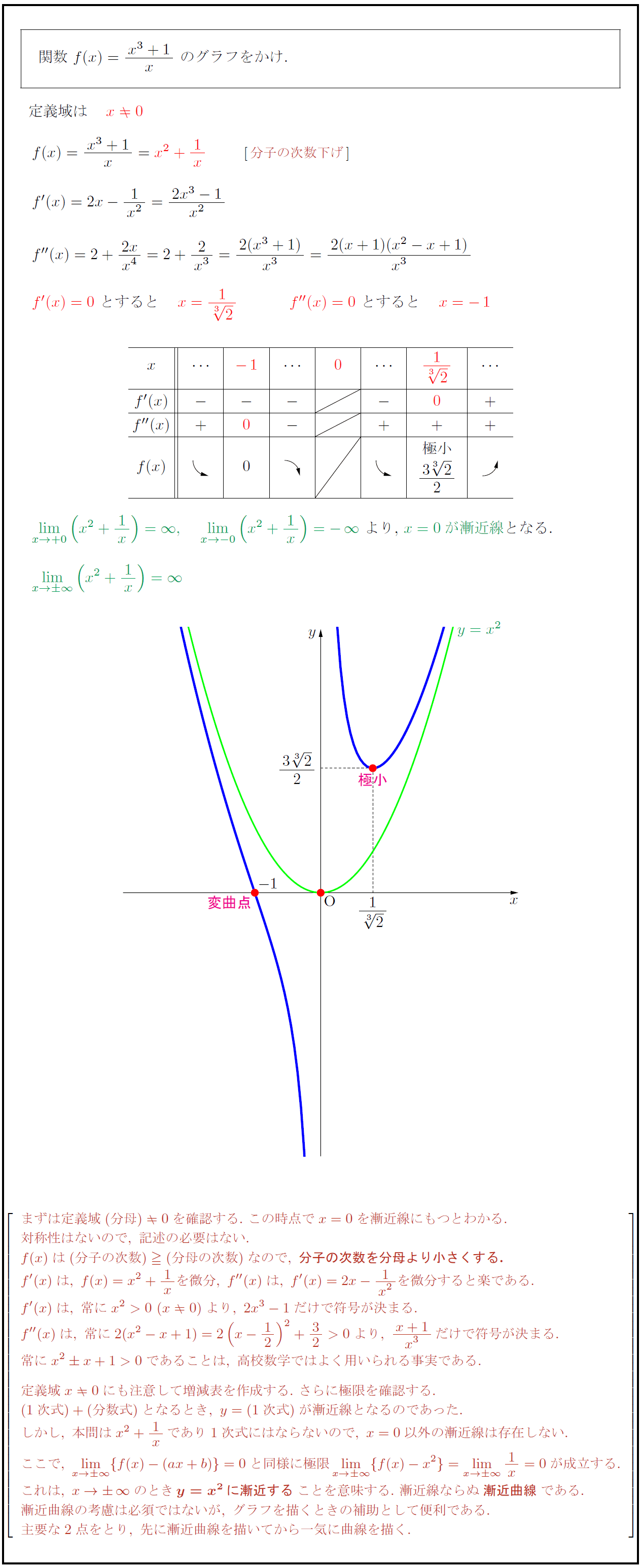



高校数学 分数関数 Y X 1 X のグラフ 受験の月




5次関数のグラフ 大阪医科大学18年前期数学第1問 理系のための備忘録



三角関数のグラフ 春日塾のブログ




中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su



方眼紙 5ミリ 10ミリ 数学の関数グラフ練習用 方眼ノート 無料ダウンロード ちびむすドリル 小学生




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ
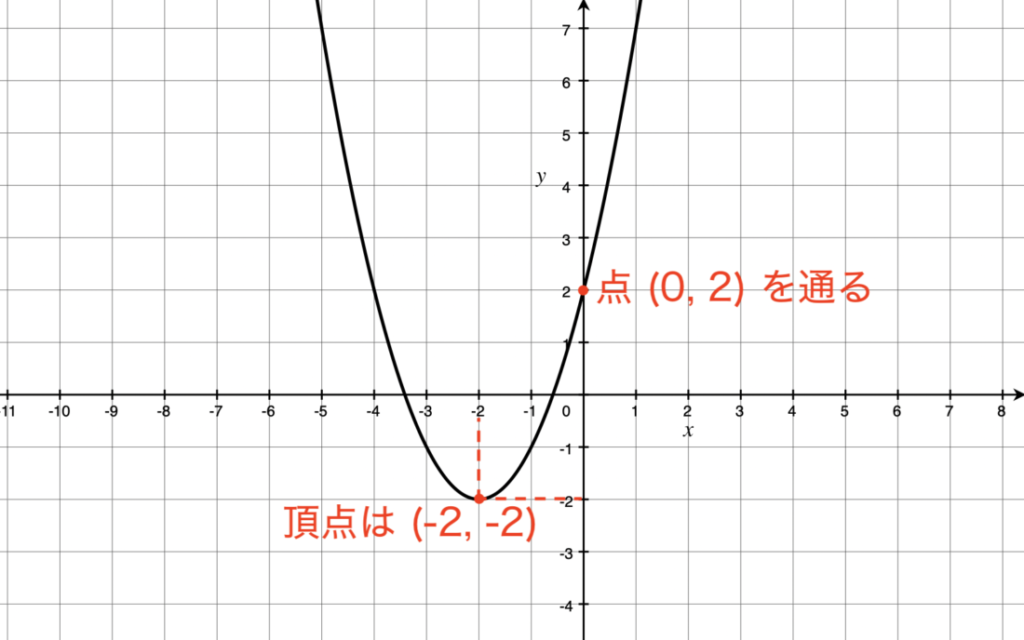



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局
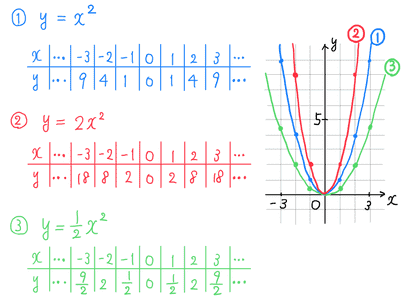



1 2次関数のグラフ ノート ひまわり数学教室
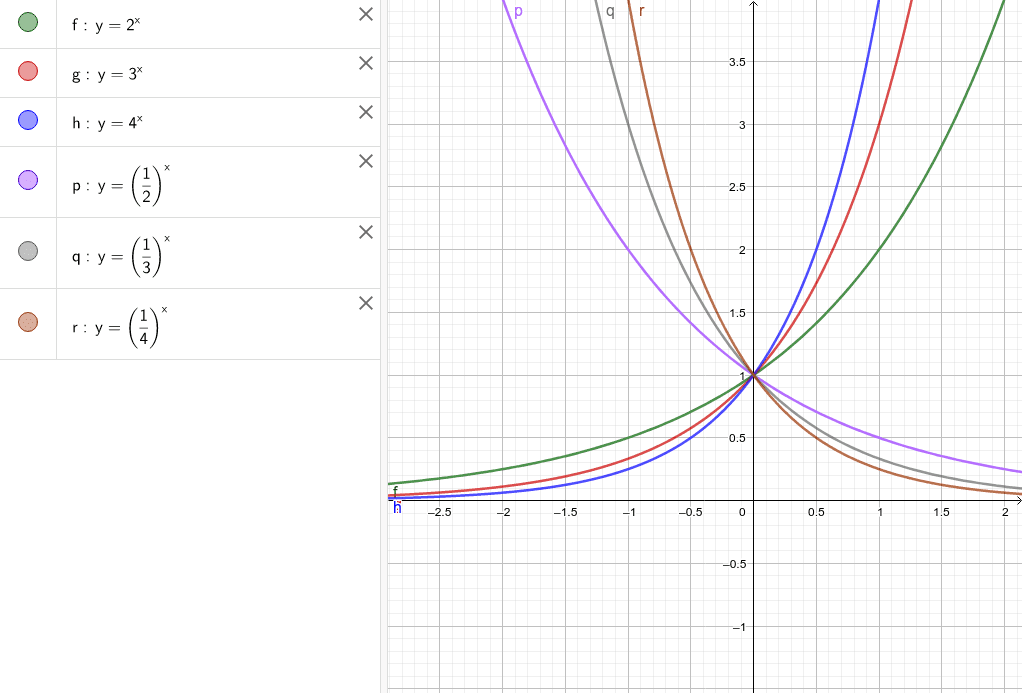



数学ii 指数関数のグラフの比較 Geogebra
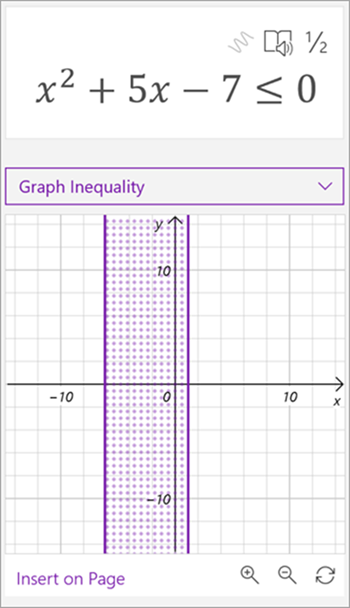



Onenote の数学用アシスタントで関数のグラフを描画する



Ib 国際バカロレア の課題 中3数学 関数グラフアート 昌平中学校 高等学校
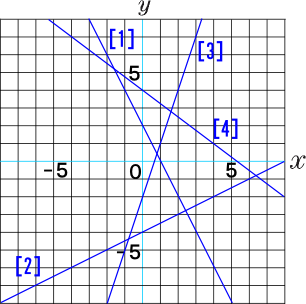



中学2年数学練習問題 一次関数の直線の式 傾き 切片 を求める問題
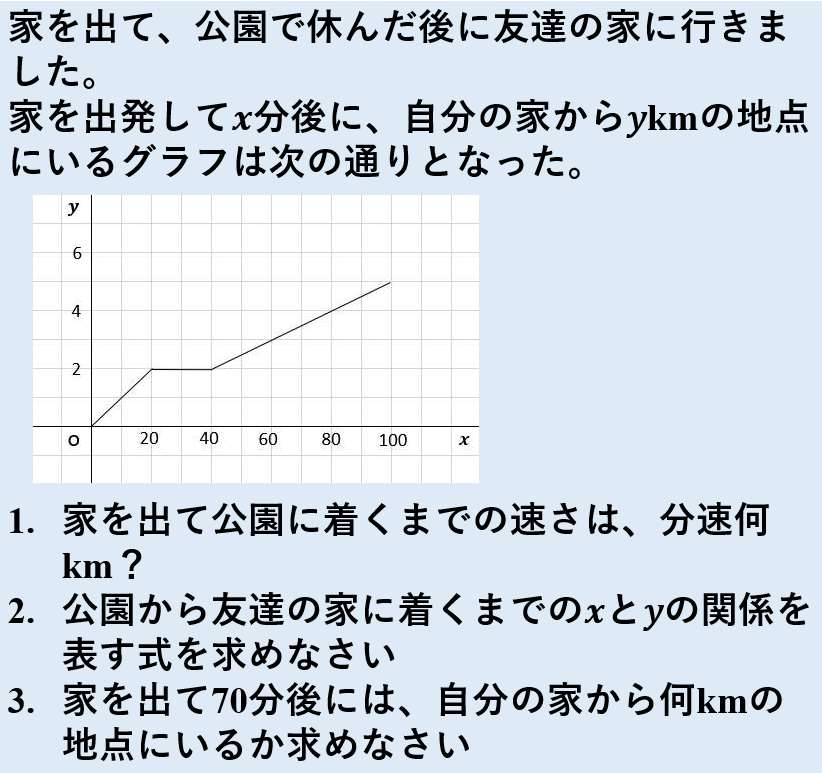



中2数学 一次関数の利用 文章題 歩く距離と時速のグラフ問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



1次関数のグラフ 中学から数学だいすき




関数用のグラフテンプレート素材 無料で使える中学学習プリント




中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
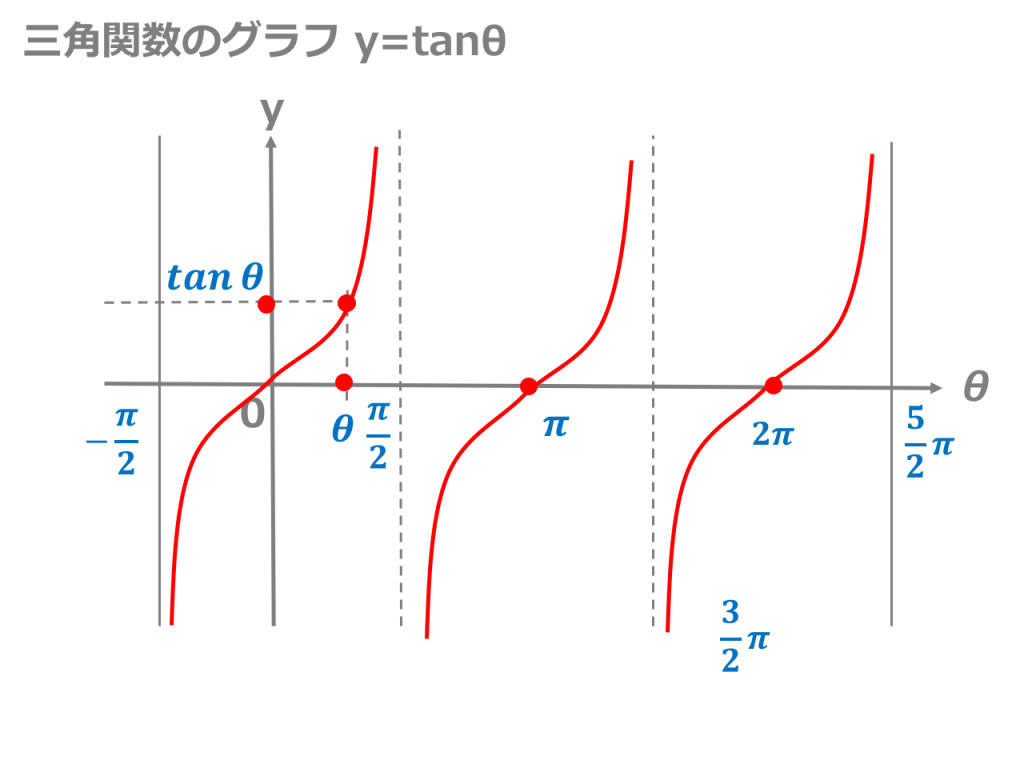



3分でわかる 三角関数のグラフの描き方 合格サプリ




中3数学 2次関数のグラフの特徴と練習問題
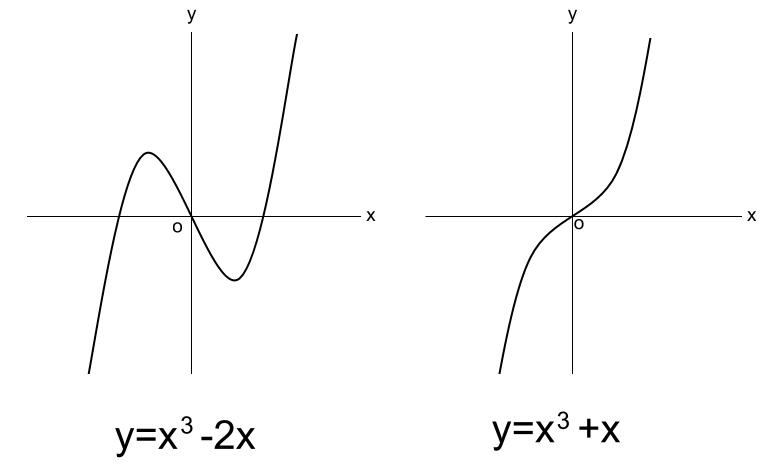



3次関数のグラフ 高校数学の無料オンライン学習サイトko Su



Wordで使える 中学数学のグラフ用紙 Wordで数学問題プリントを作ろう



48s96ub7b0z5f Net Shisuukansuu Graph
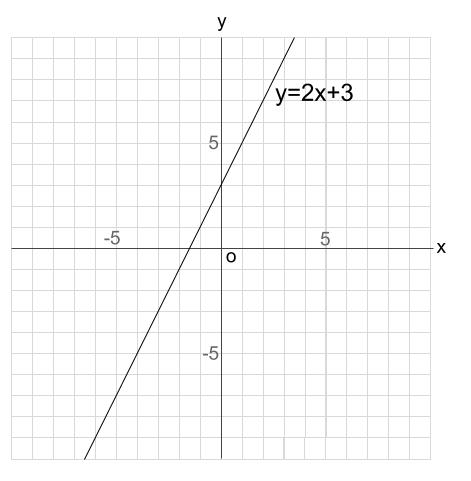



中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ
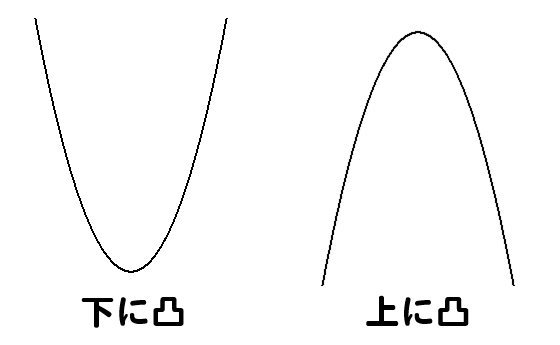



数学苦手な高校生向け 二次関数グラフの書き方を初めから解説 数スタ



数学 B 様々な三角関数のグラフ 定期テスト対策 大学入試数学の考え方と解法



数学 関数とグラフの英単語 比例 反比例 一次関数 放物線など 英単語project




高校数学 関数は グラフが命 映像授業のtry It トライイット




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく




中学 数学 関数が苦手な中学生さん 簡単にグラフを描くコツ教えます 新潟の家庭教師 ホームティーチャーズ



微分 三角関数の微分の意味 グラフで見る 大人が学び直す数学



48s96ub7b0z5f Net Sankakukansuu Graph 1



Studydoctor一次関数のグラフと傾きと切片 中2数学 Studydoctor



塾長の備忘録 三角関数のグラフの書き方




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく




一次関数とは 式とグラフの解説 数学fun




三角関数5 三角関数のグラフは縦や横から見るべし




逆三角関数



1



2次関数とは 式とグラフの解説 数学fun




一次関数のグラフ 無料で使える中学学習プリント




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




ベクトル数学関数のグラフのコレクション のイラスト素材 ベクタ Image




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット



三角関数のグラフ 周期




高校数学 三角関数の3大要素 振幅 周期 位相 とグラフの図示 受験の月




二次関数のグラフは全て相似 数学 二次関数 そーまのブログ屋さん




指数関数のグラフの特徴 数学ii By Okボーイ マナペディア
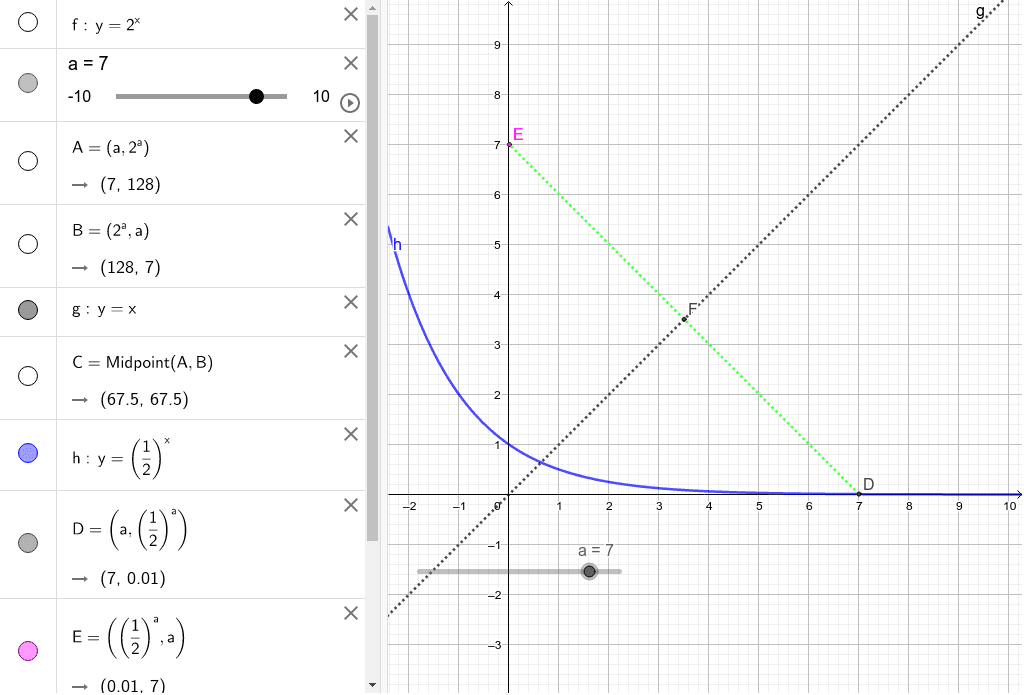



数学ii 対数関数のグラフ 逆関数 Geogebra
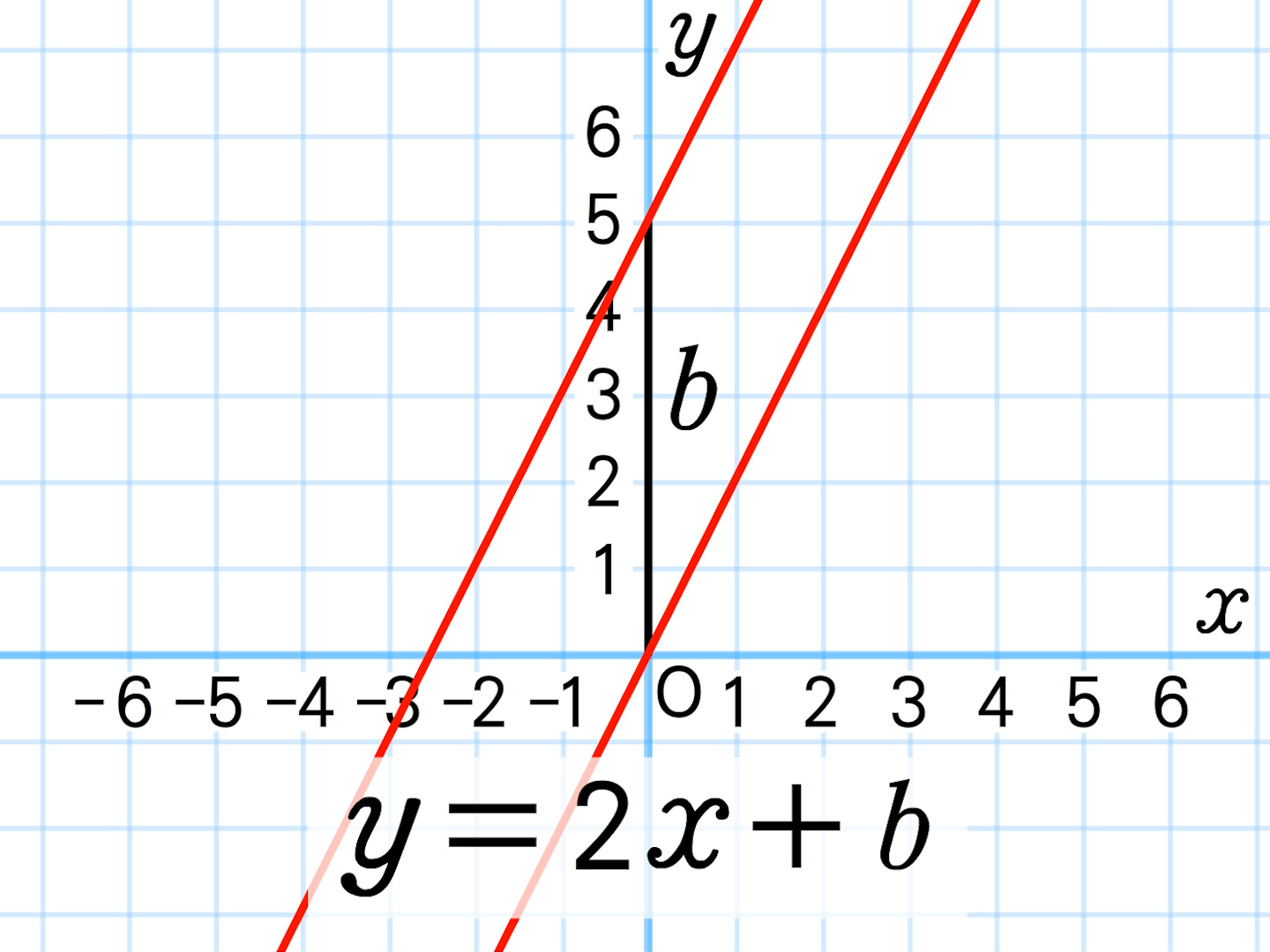



2年 1次関数のグラフ 1 数学イメージ動画集 大日本図書




中2数学 1次関数のグラフの書き方 例題編 映像授業のtry It トライイット



一次関数 二次関数のグラフや円のグラフを作成したい エクセル13基本講座




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




Recipe 各関数のグラフ 高校生 数学のノート Clear



Gnuplot S Primer
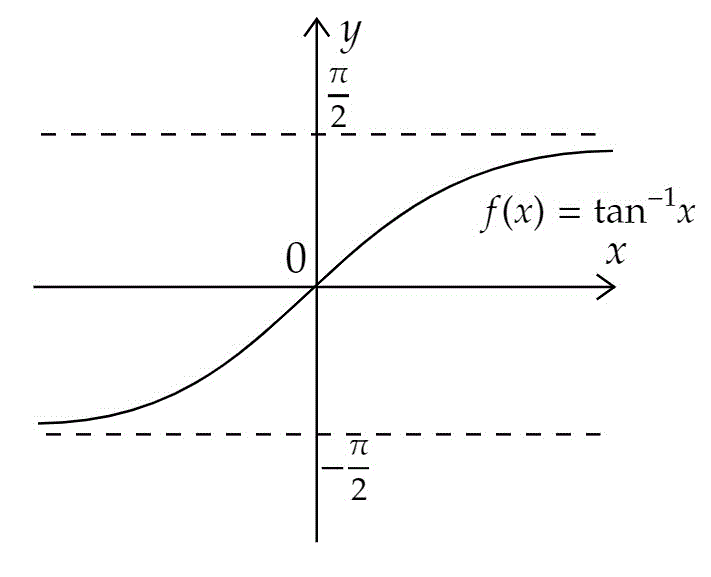



うさぎでもわかる解析 Part02 逆三角関数 工業大学生ももやまのうさぎ塾




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
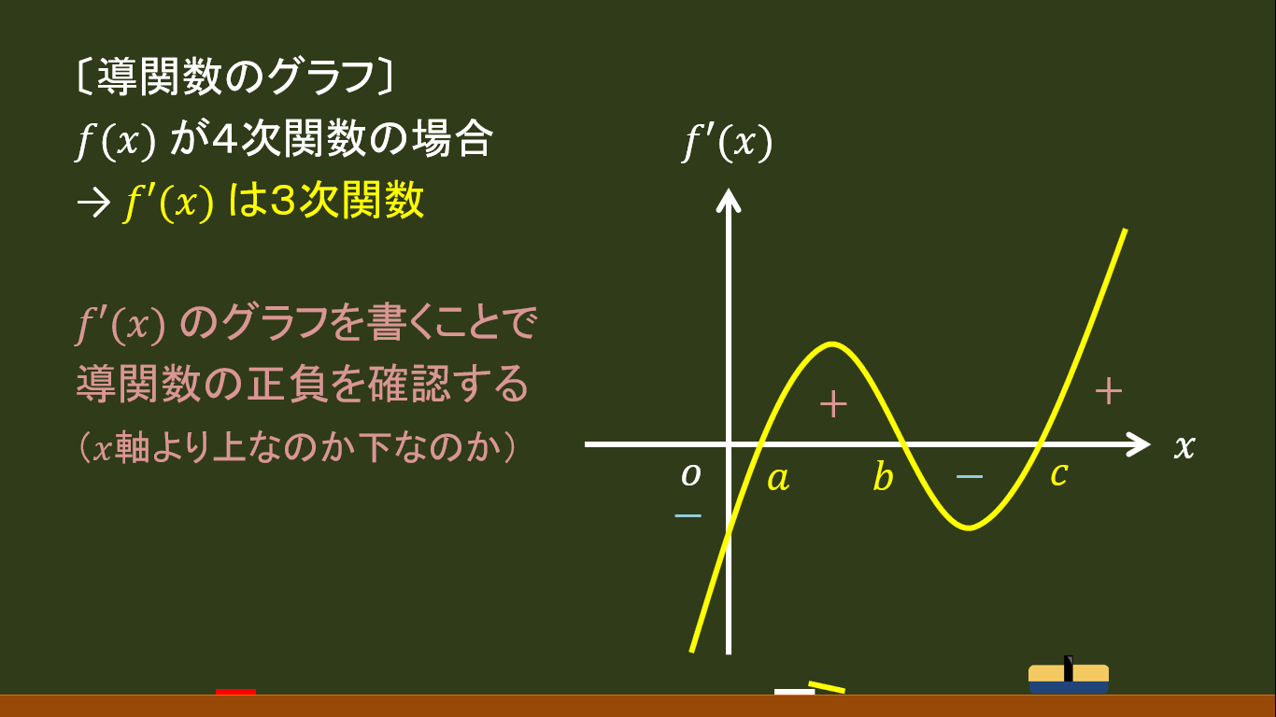



質問 数学 F X が4次関数の場合の増減表 オンライン無料塾 ターンナップ




バカでもわかる 中学数学 1次関数




いろいろな関数 無料で使える中学学習プリント




昼間から何度も質問ごめんなさい 高一の数学二次関数のグラフの問題でグラフを書く問題4 Clear
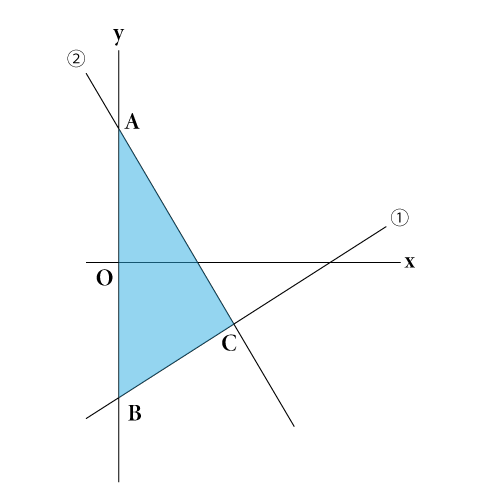



中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾



Excelでグラフ




数学 中3 35 二次関数のグラフ Youtube



1




2次関数のグラフ
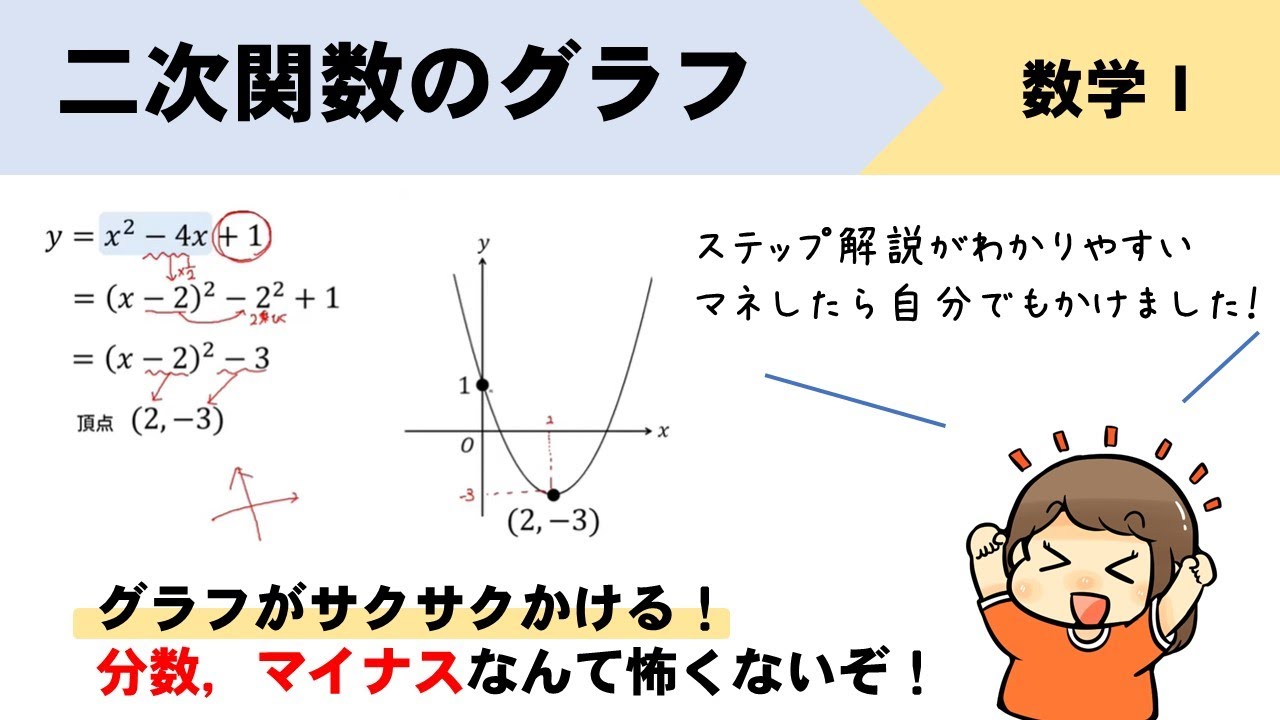



数学 二次関数グラフの書き方を初めから解説 Youtube
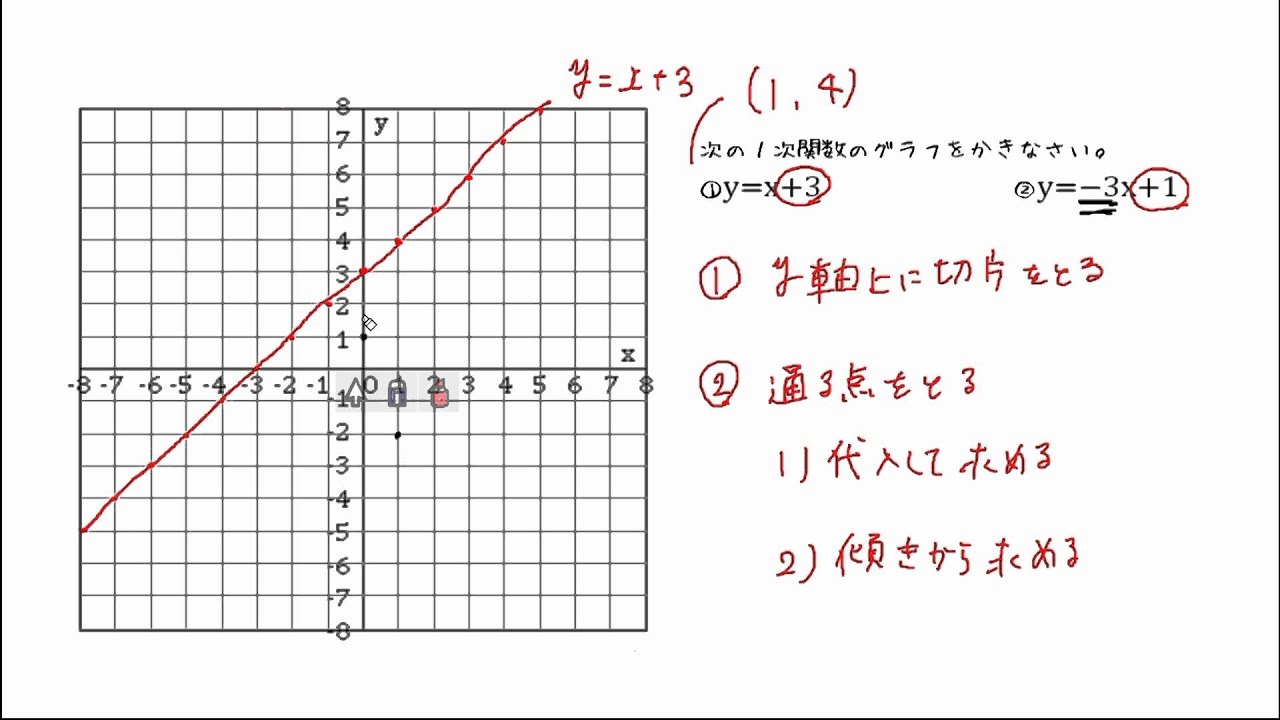



一次関数のグラフ 問題 Youtube
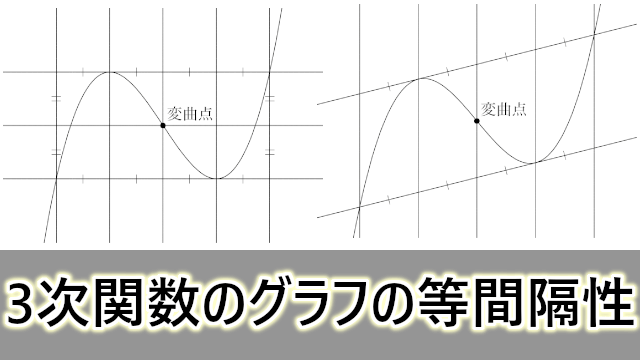



3次関数のグラフの等間隔性 大学入試数学の考え方と解法




エクセルで様々な数学的関数を学ぶ方法 グラフの作り方を解説 エクセル部




ゲルファント やさしい数学入門 関数とグラフ
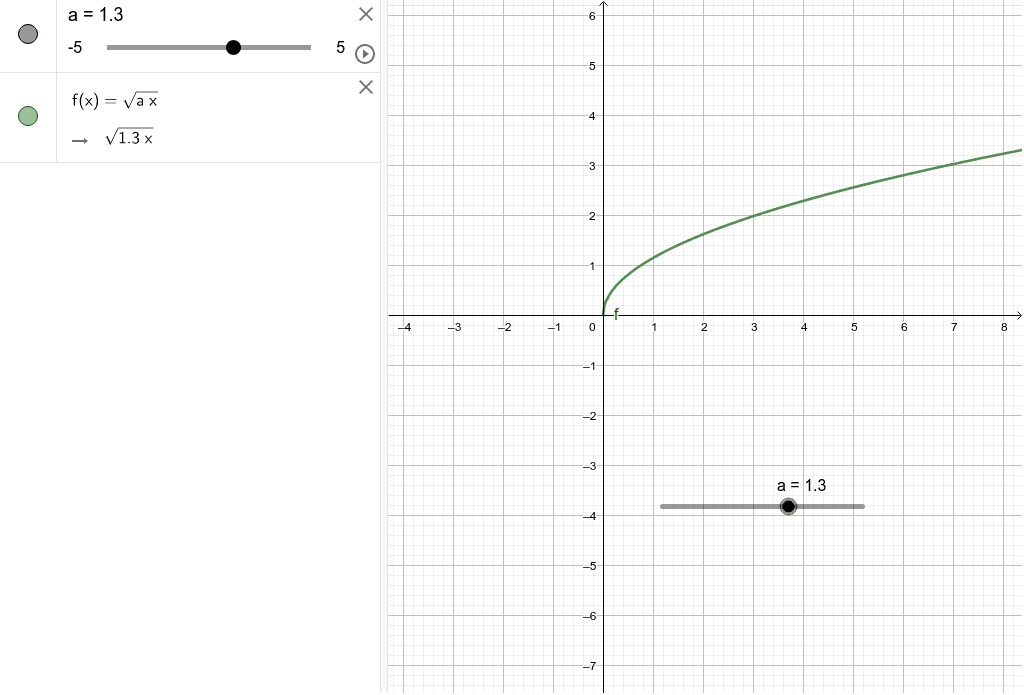



数学 無理関数のグラフの基本形 Geogebra



Ib 国際バカロレア の課題 中3数学 関数グラフアート 昌平中学校 高等学校
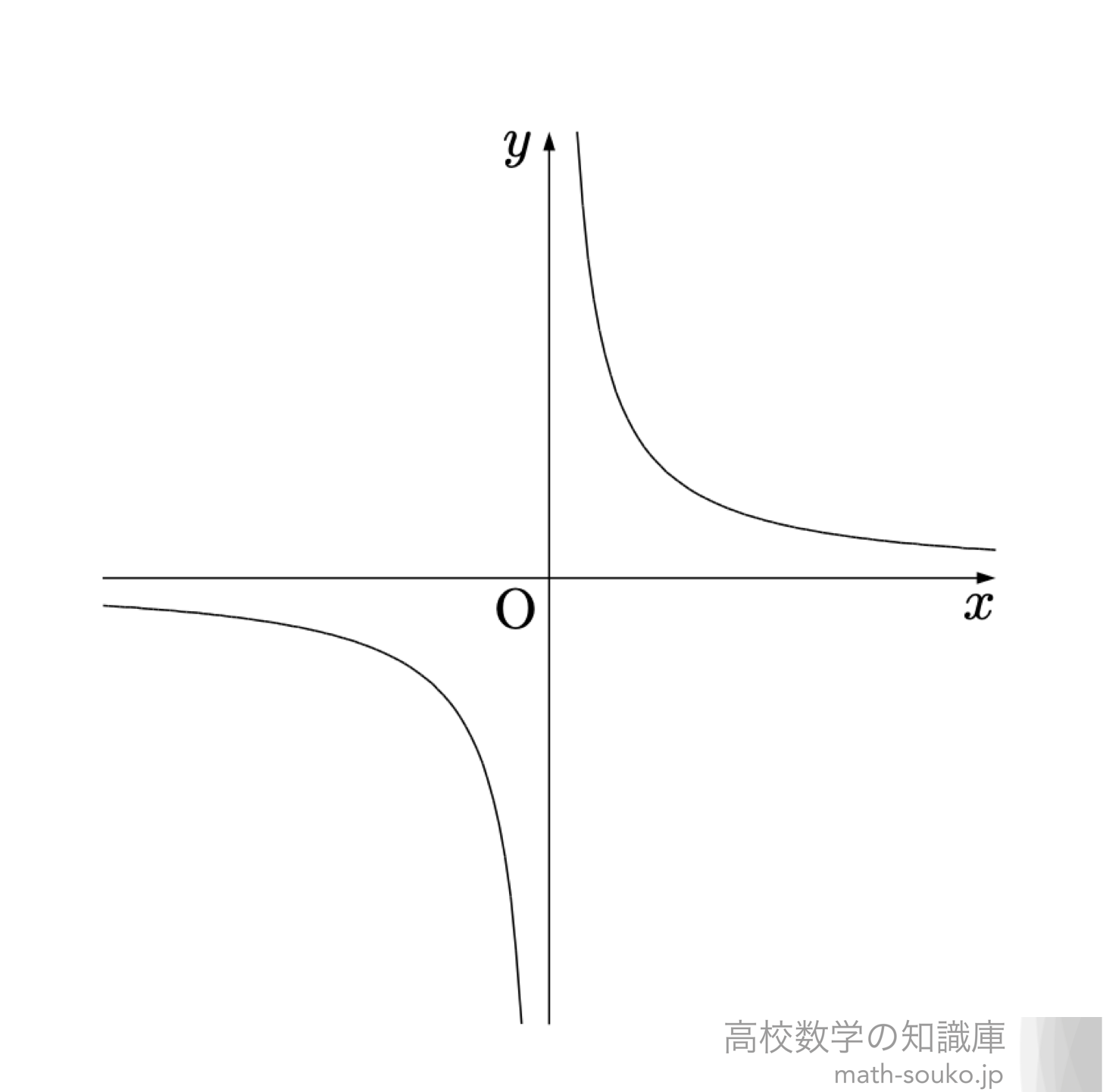



分数関数のグラフ 反比例と平行移動 高校数学の知識庫
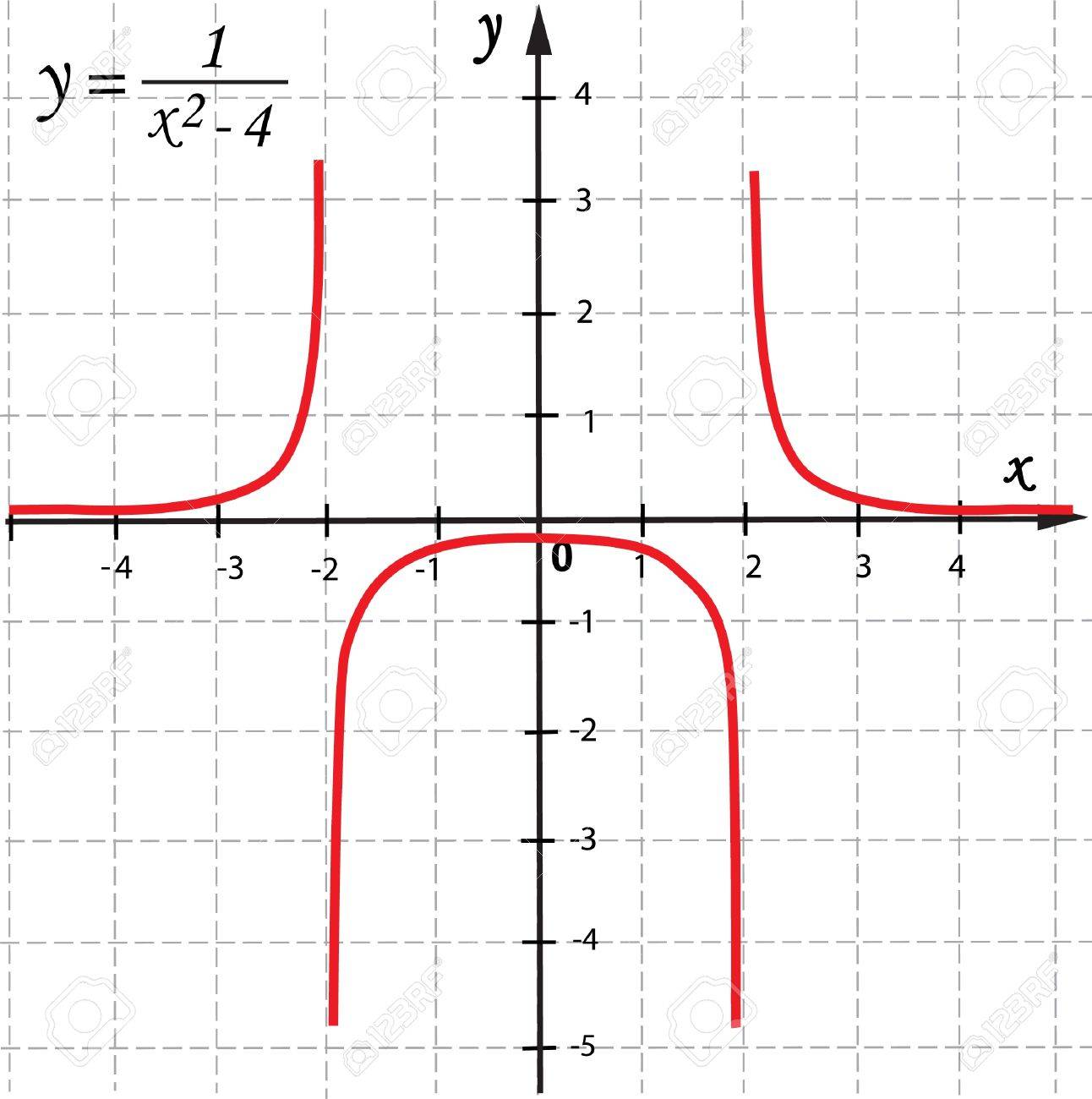



ベクトル数学関数のグラフ のイラスト素材 ベクタ Image 16
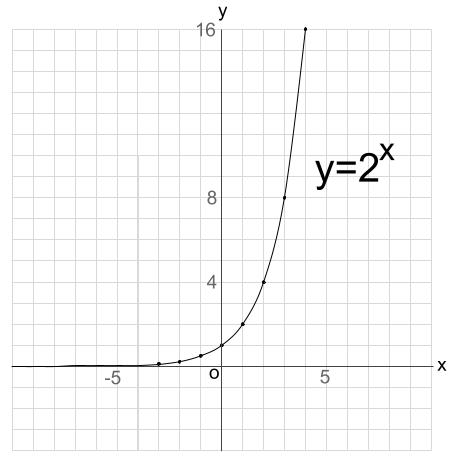



指数関数のグラフ 高校数学の無料オンライン学習サイトko Su



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師



U9j580gf8iba369ji2w Xyz P 794
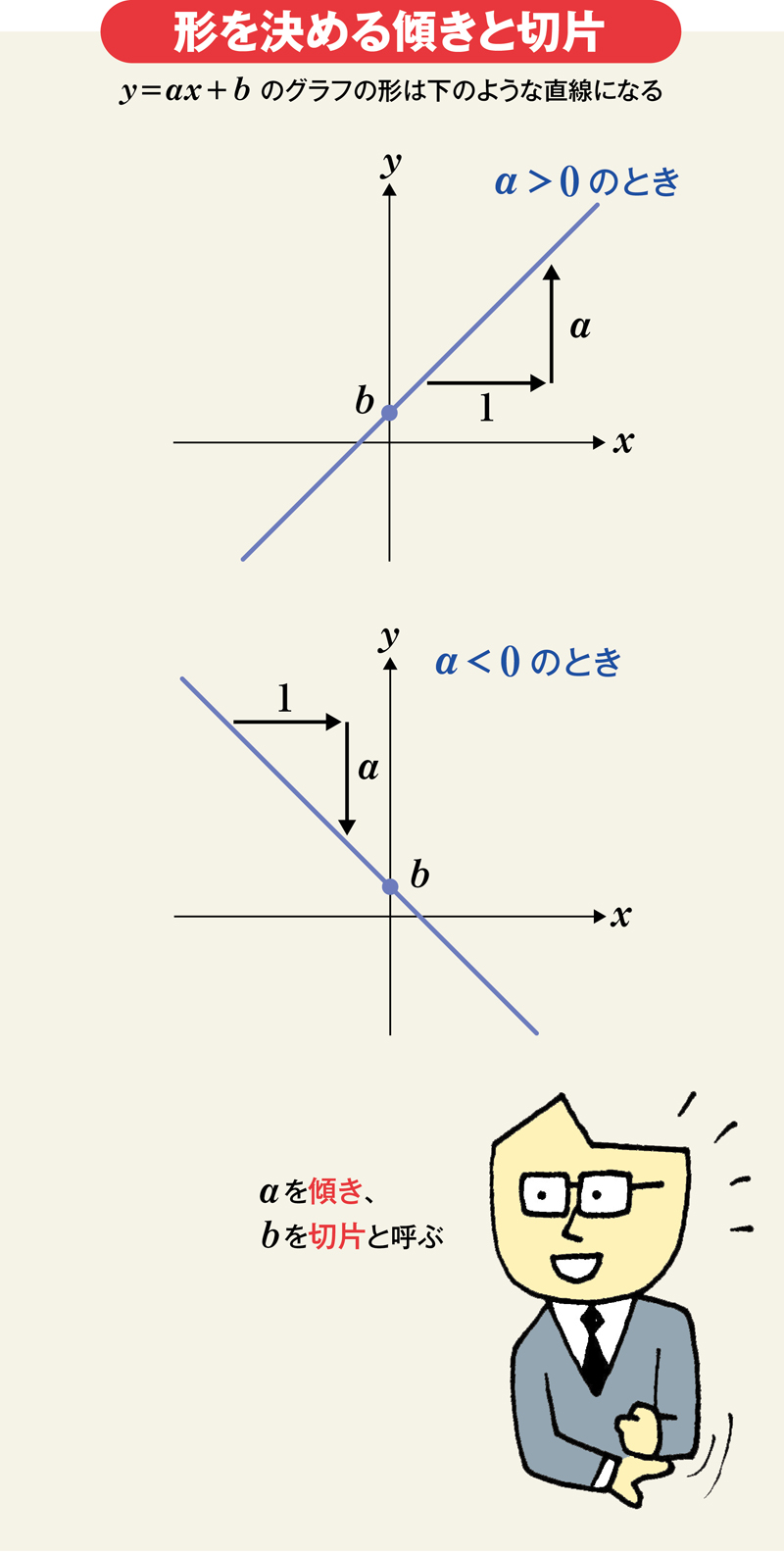



関数は 答えが出てくる便利な箱 と理解する 中高数学おさらい 1次 2次関数 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン
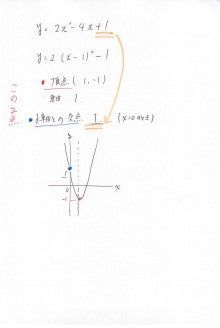



基本 2次関数 グラフの書き方 数学苦手ですorz



Excelでグラフ



Excel Vba 数学実験室 対数関数グラフを描きましょう 対数関数は指数関数の逆関数なのです



1



48s96ub7b0z5f Net Sankakukansuu Graph 2
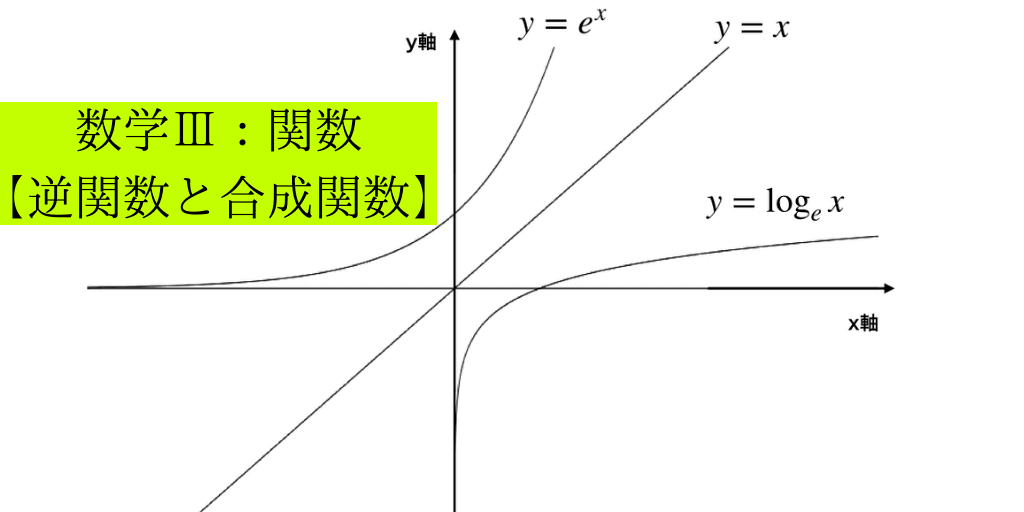



合成関数と逆関数の求め方 グラフや特徴を簡単に解説



三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典
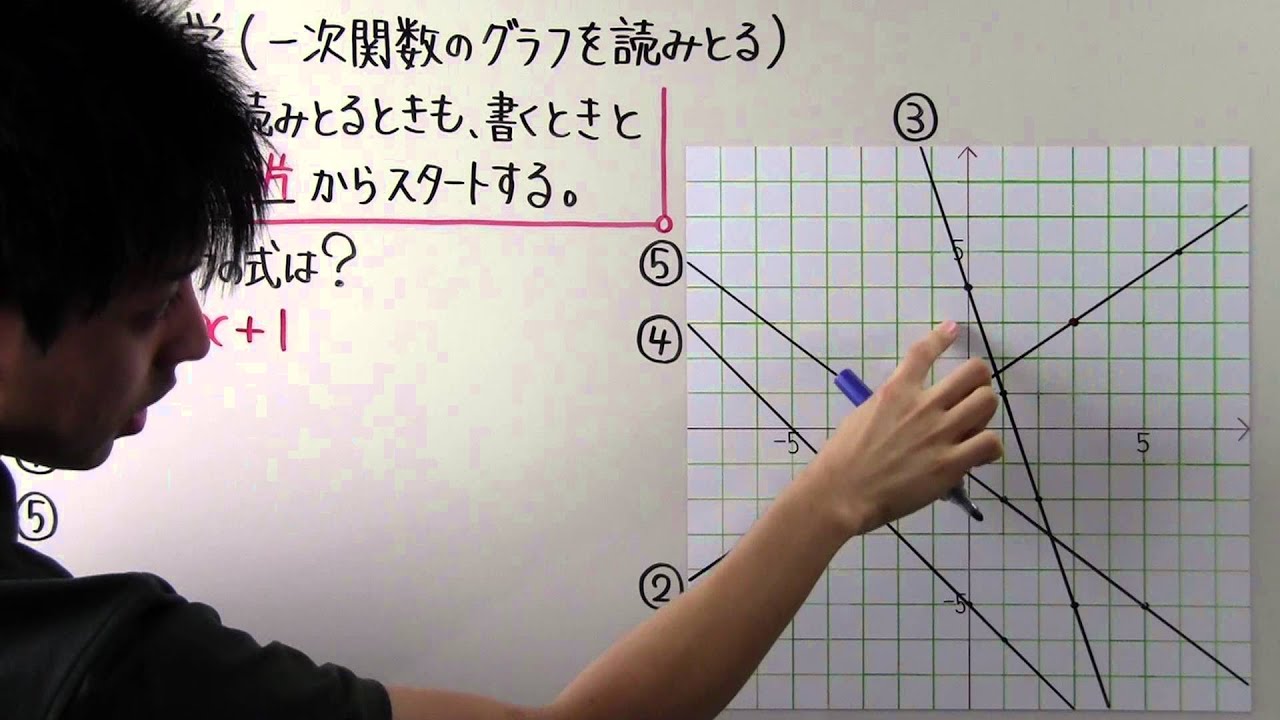



数学 中2 34 一次関数のグラフを読みとる Youtube




ピカチュウや初音ミクも 式から面白いグラフを描いてみよう
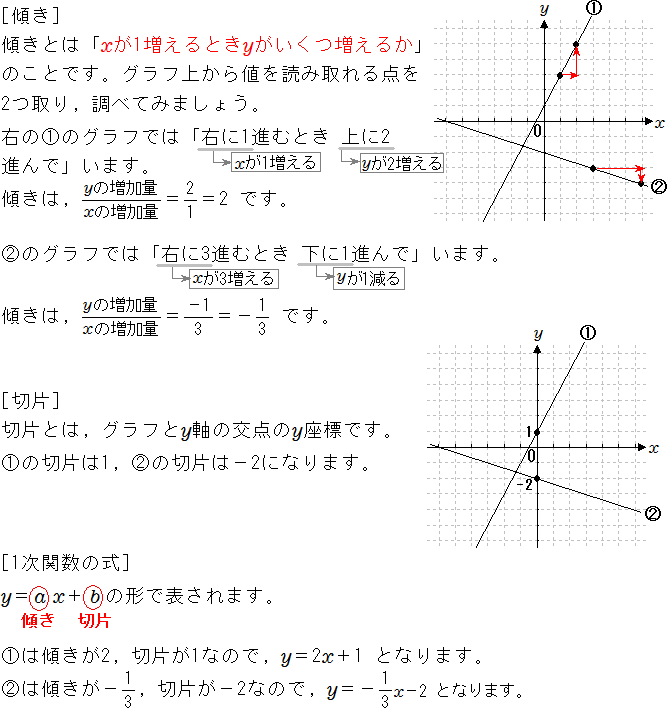



1次関数 1次関数のグラフの読み取りの基礎 中学数学 定期テスト対策サイト




中2数学 1次関数のグラフの書き方 例題編 映像授業のtry It トライイット




三角関数は2時間で解けるようになる 外資系コンサルタントが主夫になったら
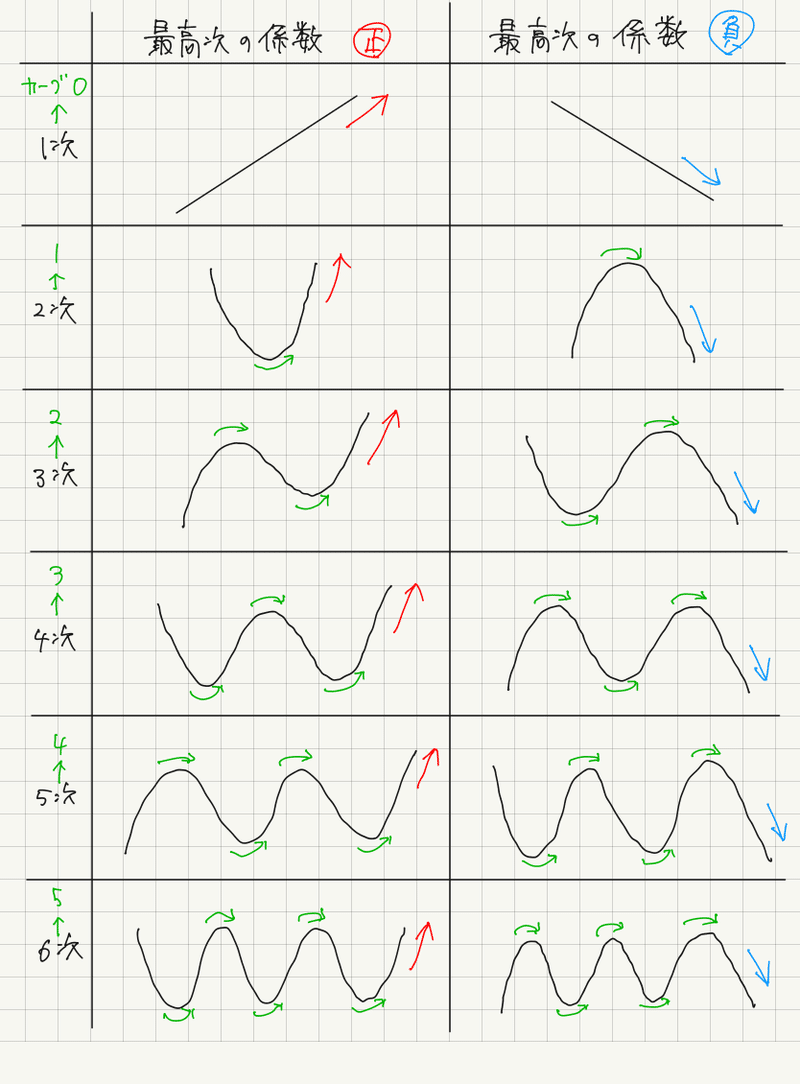



N次関数のグラフの概形 関谷 翔 Note




応用 三角関数のグラフ なかけんの数学ノート



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典




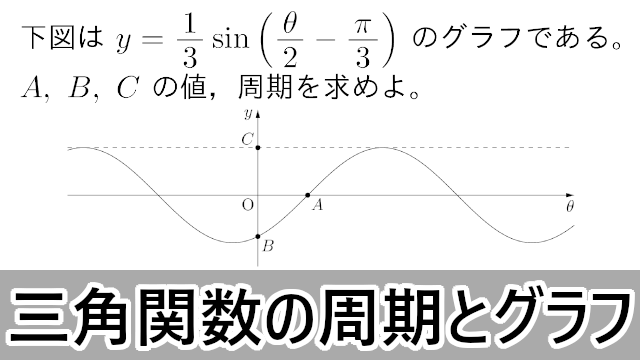
三角関数のグラフに関する問題



0 件のコメント:
コメントを投稿